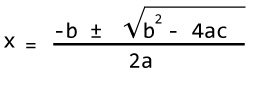For a quadratic equation ax2+bx+c = 0 (where a, b and c are coefficients), it’s roots is given by following the formula.
The term b<sup>2</sup>-4ac is known as the discriminant of a quadratic equation. The discriminant tells the nature of the roots.
- If discriminant is greater than 0, the roots are real and different.
- If discriminant is equal to 0, the roots are real and equal.
- If discriminant is less than 0, the roots are complex and different.
Program
#include <iostream>
#include <cmath>
using namespace std;
int main() {
float a, b, c, x1, x2, discriminant, realPart, imaginaryPart;
cout << "Enter coefficients a, b and c: ";
cin >> a >> b >> c;
discriminant = b*b - 4*a*c;
if (discriminant > 0) {
x1 = (-b + sqrt(discriminant)) / (2*a);
x2 = (-b - sqrt(discriminant)) / (2*a);
cout << "Roots are real and different." << endl;
cout << "x1 = " << x1 << endl;
cout << "x2 = " << x2 << endl;
}
else if (discriminant == 0) {
cout << "Roots are real and same." << endl;
x1 = (-b + sqrt(discriminant)) / (2*a);
cout << "x1 = x2 =" << x1 << endl;
}
else {
realPart = -b/(2*a);
imaginaryPart =sqrt(-discriminant)/(2*a);
cout << "Roots are complex and different." << endl;
cout << "x1 = " << realPart << "+" << imaginaryPart << "i" << endl;
cout << "x2 = " << realPart << "-" << imaginaryPart << "i" << endl;
}
return 0;
}Output
Enter coefficients a, b and c: 4
5
1
Roots are real and different.
x1 = -0.25
x2 = -1